
The old controversy around othismos
Perhaps the most important debate to understand how to fight in a phalanx of hoplites of the Greek city-states of the archaic and classical era (from the 8th to the 5th century BC) is the reference to the consideration of a compact formation where the rear rows literally push with their shields those that precede them towards the opponent with the intention of pushing them back enough to outflank them and cause a disorderly retreat where, according to sources, the greatest number of casualties occurred. in battles. This tactic was associated with the term “othismos ” (thrust) that appears in some sources, and its acceptance within the orthodox view of combat imagined the clash of hoplite phalanxes as similar to the typical collective thrust of rugby matches . In his monumental study of documented hoplite battles during the 5th century B.C. Ray (2009), for example, calculated that about 30% of victories were due to the strategy of othismos . This orthodox view, defended for example in Hanson (1989), was challenged by several authors such as Cawkwell (1978) and Krentz (1985, 1994, 2013) from various points of view:the physical impossibility of applying the othismos for an extended period given the estimated duration of the battles (which could last from an hour to almost all day), the relative defenselessness of the hoplites in the front ranks pressured to advance in such a close formation that it would not allow them to use their weapons effectively (something confirmed by recreationists in experimental archaeology ), etc. We do not intend here to summarize, as in Dahm (2010), all the details of this long and rich debate, but to apply to the case a novel analytical element that has proven useful in the strategic analysis of conflicts in many social sciences.
othismos approach via game theory
The game theory is a mathematical analysis tool that sheds light on any social situation of strategic conflict between rational agents that pursue well-defined objectives, being applied from the study of business competition in economics to politics and the study of international conflicts. Since it would be impossible to explain the mathematical details of the theory in this short essay, I will limit myself to the basic insights in this specific war context. High-quality introductory texts, such as Gibbons (1993) or Binmore (2011), are available for those who wish to delve into the subject.
The first element in a game description is to determine the rational players facing each other . In our case there would be two:Army A and B (or, if you prefer, the strategos from both). We then specify the set of strategies available for each army, both having similar characteristics and similar a priori probabilities. to win or lose the battle (both have voluntarily accepted the risk of combat):both armies face each other with two wings (left and right) and can initiate an othismos (which we denote as “1”) or not start it (“0”) with each of them independently. Action "0" consists of fighting in somewhat more open lines in which individual effectiveness is greater and recoil is possible. Thus, each army has four available strategies , depending on whether he chooses “1” or “0” with each of his wings. We can therefore represent the set of possible strategies of each army as the following four ordered pairs:(0,0), (1,0), (0,1), (1,1), where the first component of each pair represents the action of performing or not performing an othismos with the left wing (“1” or “0”) and the second component represents the same options for the right wing. Each army must, therefore, choose only one of its four possible strategies without knowing the strategy that the opponent is deciding at the same time.
We now go on to explain the consequences of each combination of strategies (or possible result of the battle). Each wing of one army faces the opposite of the other and will suffer a certain number of casualties depending on both strategies. If a wing of an army does not othismos and neither does their opponent wing, each suffers “n ” low, while if the wing without othismos faces the othismos of his opposing wing, he suffers no casualties because he moves back and causes a number “m ” kills your opponent. On the other hand, two opposite wings in othismos no significant casualties are caused either. Also, if one of the wings of an army (let's say it's A) doesn't do othismos and the other does, while the other two opposing wings do the same action (either “1” or “0”), then Army A will be flanked and panicked with uncontrolled withdrawal. In that situation, army A as a whole will suffer “M ” Additional kills to the ones he already had on each of his wings. We know from the sources that this is the situation where more casualties occur , so we assume that M> m> n> 0. Those are all the parameters we need to describe the strategic situation of our game.
The table 1 collect the losses that each army will suffer in each of the possible situations of the game. We assume that army A selects a single row from the table and army B selects a single column. The first number in each cell is the number of total casualties suffered by Army A, and the second number is the number of casualties suffered by Army B for that strategy choice.

Now we must answer the question of what objectives it is reasonable to assume to each player/army. A reasonable goal would be to maximize the difference between the opponent's total kills minus your own. The greater this difference, the greater the victory in relative terms that army will be able to claim against its rival. Let's call that difference the “utility” of the corresponding army , which will serve as a quantitative measure of the degree of achievement of its military objectives. We can visualize the utility that army A (which chooses ranks) will receive in each possible situation of the game in table 2 .
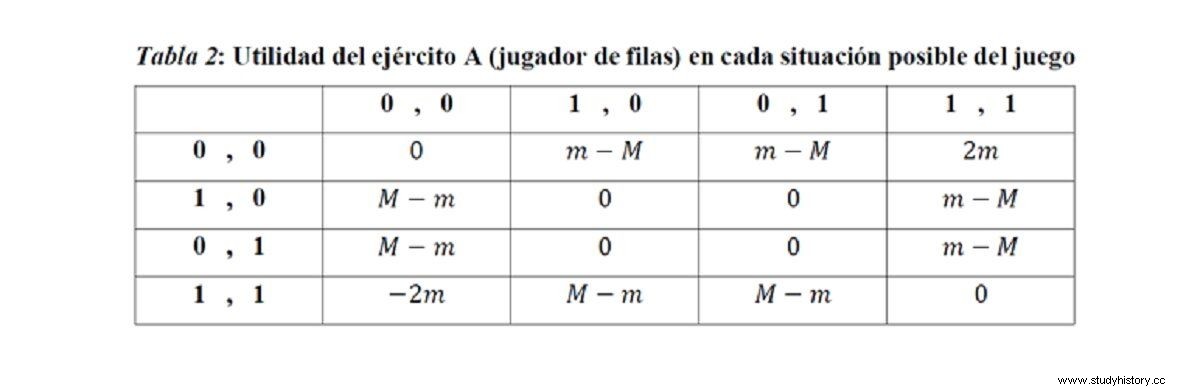
Note that the sum of the utilities of both armies for each possible result of the battle is always zero, and whatever one army wins the other loses . This is what is called a "zero sum game", typical of situations of extreme conflict.
We now turn to the solution prediction of the proposed game. If both armies are rational in the sense that they want to maximize their respective utility (and thus minimize the enemy's) and know that their enemies are also rational, what strategies can each be expected to choose in the battle game? ? The solution concept that applies to this type of game is known as “Nash equilibrium” . A combination of strategies for both players (a cell in table 2 ) is a Nash equilibrium if each player is maximizing his utility given the opponent's equilibrium strategy. Both players would therefore be doing their best for each other in a compatible way.
If we look at table 2 , it is clear that the best strategy of army A if the other does not exercise othismos with no wing ((0,0), first column) is to carry out the othismos with only one of its wings (choose either (1,0) or (0,1)), with which it manages to break the enemy's front and cause "M + n ” kills at the cost of suffering only “m + n ” low (“m ” of the wing in “1” and “n ” of the wing to “0”). On the other hand, if the enemy were to adopt any of the strategies that could potentially break our ranks before (0,0) (i.e. (1,0) or (0,1)), second or third column of the table), Army A's best response would become othismos in the two wings (1,1), with what would be the army that breaks the ranks. It would seem for the moment that the othismos goes to account However, if the enemy were to opt for othismos total (1,1), it turns out that the best strategy for our army is precisely (0,0). It is true that it will push us back, but our ranks will not be broken and we will be causing them more casualties per wing (“m ”) of those caused by him (0), due to the greater efficiency in combat of action 0 (do not do othismos ).

Thus, we can conclude that no there is no combination of strategies (cell of table 2 ) such that the strategy of each army is the best response to the one carried out by the other , and there is no Nash equilibrium as stated above. Does that mean that there is no rational way to make decisions in this game? If we only contemplate what is known as "pure strategies" (choosing a single row or column from table 2 ), there is certainly no solution to the game, but if we admit that both armies can choose their strategy by “rolling the dice” (choose strategies following a certain law of probability), then there is a Nash equilibrium in “mixed strategies”. Choosing strategies by "rolling the dice" might seem unserious in a war situation, but it's not at all . Moreover, this is precisely what we should expect in symmetric zero-sum conflict situations where each strategy is optimal against another of the rival.
Let us consider the game of “rock, paper and scissors”, where the same phenomenon concurs:how should we choose strategy? If our opponent knew that we have a slight tendency to pick “rock” more often than the other options, his best bet would always be to pick “paper” against us, and he would end up beating us more often than we beat him. To avoid this, the only thing we can do is balance the probabilities of choosing the three strategies . Avoiding predictability as much as possible is the best strategy for each player, so the Nash equilibrium occurs when both players choose each of the three options completely at random and with equal frequency. The same happens in the case of the game of results of a soccer penalty where the striker can shoot to the left side of the goal or to the right and the goalkeeper of the rival team, in turn, must choose which side to shoot to. A good striker should shoot to each side 50% of the time, and with the same probability the goalkeeper should shoot, strategies that have extensive documentary support (Palacios-Huerta (2003), Azar &Bar-Eli (2011)).
How do you find the optimal probabilities of the Nash equilibrium of the game summarized in table 2 , then? Basically it is a question of choosing probabilities so that each of the pure strategies of army A provides the same expected utility as the others, given the probabilities with which the enemy plays its pure strategies. It takes a little algebra to get to the final result, but if we call 𝑝1, 𝑝2, 𝑝3 and 𝑝4 =1 − 𝑝1 − 𝑝2 − 𝑝3 the probabilities of choosing the strategies (0,0), (1,0), (0,1) and ( 1,1) respectively for player 1 at equilibrium (the symmetry of the game guarantees that they will be the same for player 2), the unique Nash equilibrium in mixed strategies requires choosing strategies with the following probabilities:
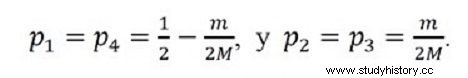
Note that the parameter that measures human losses when two opposing wings do not othismos , “n ”, is irrelevant in the selection of strategies and, in fact, the optimal frequency of choice of strategies depends only on the ratio m /M . It is also interesting that the strategy (0,0) is always chosen with the same frequency (𝑝1) as the strategy (1,1) (𝑝4). In addition, it can be concluded that, the greater “M ” or less “m ”, higher frequency of othismos strategies total (1,1) and not othismos total (0,0), since the first one becomes more profitable by causing with greater probability the breaking of the opposing force when it performs othismos partial, but also, as a response to this increased frequency of (1,1), the opposite strategy (0,0) also becomes more profitable. On the other hand, if the casualties caused by the more open lines against an opponent in othismos were increased (“m ”), logically increases the profitability of not doing othismos , but only in the partial cases (1,0) and (0,1), while (1,1) becomes less frequent and, as a consequence, also (0,0). Ideally, this mathematical model could be tested with the frequencies observed in ancient phalanx battles, although to extract the logic of the equilibrium strategies we have had to simplify many other factors that have been decisive in the real result of many battles, such as differences in the terrain, in the total number of troops available for each side and their quality, the presence of other types of units such as peltasts, cavalry, etc.
Conclusions
With this theoretical contribution I have tried to defend that, extracting the basic elements characteristic of hoplite phalanx battles and taking them all for granted, the deep strategic logic of the confrontation does not can produce a single functional winning strategy (the othismos across the line or its opposite, a pushless engagement with more open lines), but precisely predicts the diversity of strategies actually employed in the line of battle. In fact, assuming that during the battle you can rethink strategies on the wings, what would be expected would be the type of fluctuations between othismos and more open lines without pressure to advance in different sections of the battle line, which has already been proposed by authors such as Matthew (2009) or Dahm (2010). In particular, the othismos represents an effective way to break the enemy line , flank it to induce panic and cause its disorderly withdrawal only if it is exercised from either of the two wings, but not from both at the same time as a single tactic, which seems to correspond to an unequal arrangement of the number of rows in the wings which has been documented in battles such as Leuctra (371 BC). This functionality is maintained even if kills in the first rows of a wing apply othismos may be far superior to what they would have with a more open formation that allows more effective use of weapons (m> n ). The potential benefit of breaking the enemy line simply offsets that cost in casualties (M> m ). Thus, the heavy infantry panoply in a hoplite battle need not be optimized for the combat survivability needs of frontline hoplites.
Bibliography
- Azar, O.H. &Bar-Eli, M. (2011), “Do soccer players play the mixed-strategy Nash equilibrium?”, Applied Economics 43:25, 3591-3601.
- Bardunias, P. “The aspis . Surviving Hoplite Battle”, in :Ancient Warfare I.3 (2007), 11-14.
- Binmore, K. The theory of games. A brief introduction , Publishing Alliance, 2011.
- Cawkwell, G. L. Phillip of Macedon . London 1978.
- Dahm, M. “The shove” or not the “shove”:the othismos question”, in:Ancient Warfare IV.2 (2010), 48-53.
- Gibbons, R. A first course in game theory , Antoni Bosch Ed., 1993.
- Hanson, V.D. The Western Way of War . Oxford 1989.
- Krentz, P. “The Nature of Hoplite Battle”, Classical Antiquity 16 (1985), 50-61.
- Krentz, P. “Continuing the othismos on the othismos”, Ancient History Bulletin 8 (1994), 45-49.
- Krentz, P. “Hoplite Hell:How Hoplites Fought”, in Men of Bronze:Hoplite Warfare in Ancient Greece , Kagan, D. &Viggiano, F. eds., Princeton University Press, 2013 [en esp. Men of bronze. Hoplites in ancient Greece , Awake Ferro Editions, 2017].
- Matthew, C. A. “When Push Comes to Shove:What was the Othismos of Hoplite Combat?”, in:Story 58 (2009), 395-415.
- Palacios-Huerta, I, “Professionals Play Minimax”, Review of Economic Studies 20 (2003), 395-415.
- Ray Jr., F.E. Land Battles in 5 th Century BC Greece. A History and Analysis of 173 Engagements , McFarland, 2009.
- Ray Jr., F. E. Greek and Macedonian Land Battles of the 4 th Century BC Greece. A History and Analysis of 187 Engagements , McFarland, 2012.
