A cow and a horse start off from the same point P in different directions. Both travel circular paths that converge at point P. If the cow advances along a path A of 48 km. in circumference at a speed of 8 km. a day, and the horse a path B of 32 km. of circumference to 12 km. per day, how many days will it take to meet again at point P?
Let's see, raise your hands readers to whom phrases like this cause a chill. And it is that, for those of us who are letters, as is the case of the person who writes these lines, it is not strange to have nightmares, even today, with the calculation or arithmetic problems that they taught us at school. But, as there has to be everything in this world, there are also people who enjoy playing with numbers. Hence the tremendous success of sudokus in recent years, for example. A pastime in the form of arithmetic boards that fascinates lovers of mental calculation and drives the rest of mortals upside down. Although this type of numerical puzzle is not, strictly speaking, a Japanese invention, it has been the Japanese who have given it its definitive form and have popularized it throughout the world under the name of sudoku .
If we go back a few centuries, we see that solving mathematical problems to kill time is nothing new. In the land of the rising sun, these pastimes have a long tradition dating back to the time when samurai walked the streets with their katanas on their belts. In the mid-eighteenth century, among the votive tablets that the faithful offered at the doors of shrines and temples throughout Japan, it was also common to find things like the problem that heads these lines:
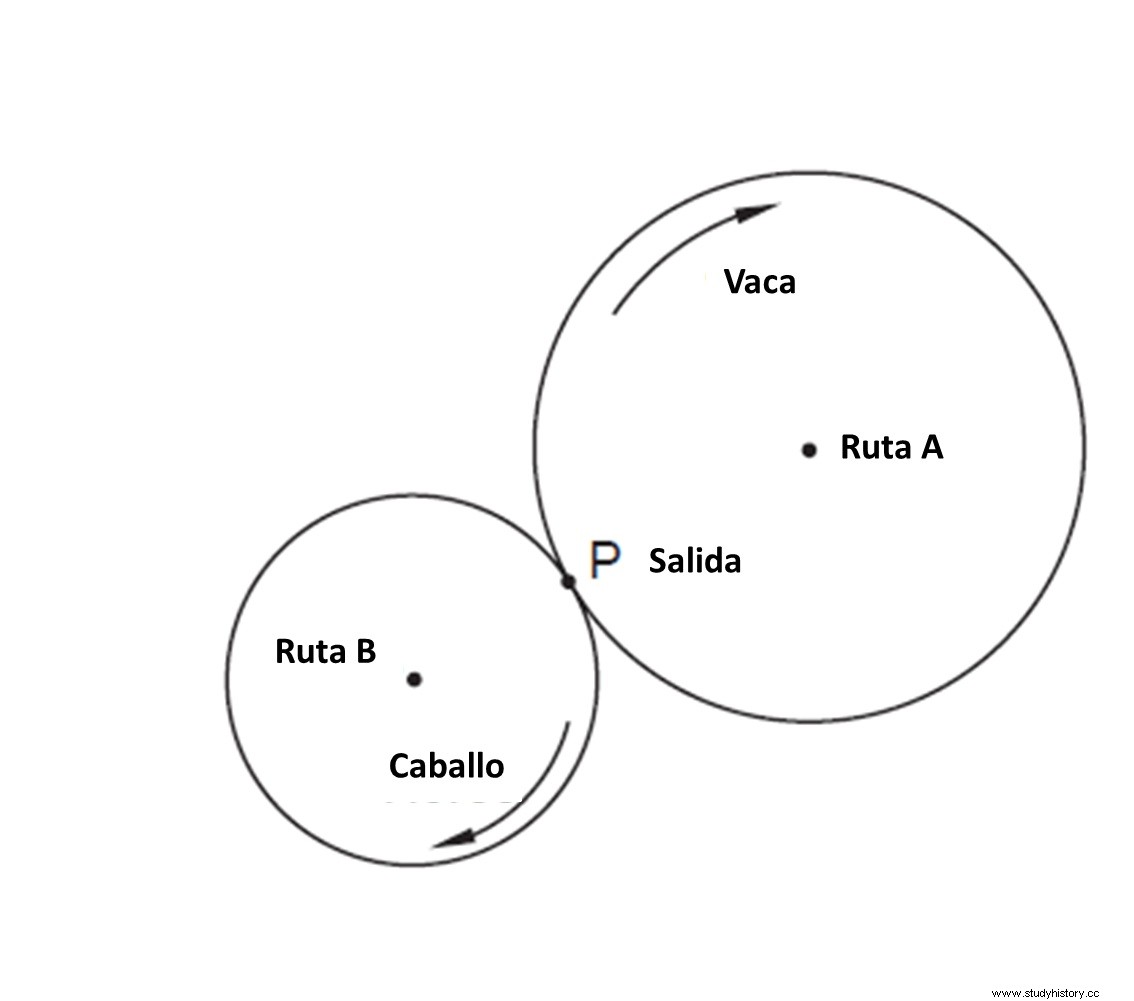
How many days will it take for the cow and the horse to meet after leaving point P?
Does any brave dare to solve the enigma? For those less adept at geometry, the solution can be found at the end of the article.
It could be thought that these problems were hung there, at the door of the temples, to invoke divine help, because to solve such gibberish someone would need the help of a couple of gods and the odd Buddha, at the very least. But no, that was not the reason. Actually, these tablets were just a hobby. And, at the same time, a challenge for restless minds, waiting for someone to be able to find the solution. That is why they were left in the most public place possible, where everyone, noble or commoner, passed:the door of the temples.

The Japanese of the time had a name for these arithmetical puzzles. They were called sangaku , which came to mean "mathematical tablet". The word even reminds modern Sudoku puzzles. These sangaku tablets They contain very precious drawings to support the statements of the problems, since traditional Japanese geometry was a mixture of art and mathematics. It's part of its charm; In addition to serving as mental gymnastics, they fulfilled a decorative function. Unfortunately, the fact that they are made of wood has meant that few of them have survived the passing of the centuries. But those that have been preserved give us a good perspective of what this ancient tradition was like..

In Japan at the time, in the midst of the Tokugawa shogunate, the development of mathematics was not the exclusive domain of the academic world. Scholars and common people alike devoted themselves to cultivating them enthusiastically. So these sangaku tablets were the work of math enthusiasts who, completely anonymously and for the love of art, left them at the entrance to shrines. The objective was, simply, that whoever passed by and had some free time would be entertained by solving the problems they posed.
Much of it is based on the Pythagorean theorem, which was known to the Japanese of the Middle Ages thanks to the knowledge that came from China centuries ago. Most sangaku can be solved either with this theorem or by using square equations. But even though the tablets told you the solution at the end, they usually never detailed how to get to that solution. They had to figure this out on their own. It was a kind of intellectual challenge, a challenge from the anonymous author to anyone who wanted to accept it.
It is believed that the authors of these tablets were mostly people of the samurai caste. At this time, with the Tokugawa dynasty ruling the newly unified Japan, there are no more civil wars to fight, so the samurai, the warrior nobility, have to adapt to the new times. Many of them exchange the sword for the abacus, becoming schoolteachers teaching village children to read, write, and do math. This is how, isolated from the outside world and oblivious to European scientific progress, the Japanese began to develop mathematics on their own. Advancing along different paths than those of the Chinese and Western sages to reach similar conclusions. And these village mathematicians, simple people without many means, who did not have access to the academic world and could not afford to publish their discoveries in standard treatises, resorted to the sangaku tablets to show the world their progress.

It is not known exactly when this fashion of sangaku began, but the oldest surviving date from 1683, and there are testimonies that mention the existence of these tablets from almost the beginning of the 17th century. The tradition lost steam with the fall of the Tokugawa shogunate at the end of the 19th century, but in one way or another it has endured almost to the present day. The last known sangaku date back to the 1980s.
The millions of sudoku enthusiasts around the world will surely like to know that their favorite pastime is part of an ancient tradition. Because, as we can see, the Japanese have been inventing mathematical puzzles for centuries. Although to some of us, who do not give us the head for so many numbers, this sangaku seems more like a form of torture disguised as colored circles.
Solution to the previous problem:
After a number of days D, cow and horse meet again at point P. If the cow advances 8 km. per day and completes a certain number of laps, then we have 8D =48M, where M is the unknown to solve. Similarly, in the case of the horse 12D =32N, where N is another unknown. Dividing both equations we obtain M/N =4/9 but, since we are looking for the smallest possible value for the unknown, we can keep M =4 and N =9. Therefore, D =24 days. A piece of cake, right?
Contributed by R. Ibarzabal of Samurai Stories
Sources:Sacred Mathematics , Fukagawa Hidetoshi and Tony Rothman; Sangakus
